Math(s) can be a tricky subject for many students. But some questions are trickier than others.
Put on your thinking caps because we searched the internet for the top 5 trickiest mathematics questions from all around the world.
Solutions are provided at the end of all the questions (but no peeking).
If you’re up for an extra challenge, we’ve even got a bonus question at the end.
But before that… a quick announcement. World Maths Day – the world’s largest mathematics competition is back!
World Maths Day, happening on 8 March 2023, is a global celebration of mathematics where millions of students aged 5 to 18 across the world compete in Live Mathletics challenges. It’s all-inclusive, free, and open to schools as well as students learning from home. Learn more about it here.
Now, let’s jump in!
1. People on a Train 🚂
Country of origin: England
In a since-deleted tweet, a mum from England tweeted this word problem in a test meant for kids aged 6 to 7 in 2016. It went viral and even some adults were having trouble figuring out the answer.
The Question:
There were some people on a train.
19 people get off the train at the first stop.
17 people get on the train.
Now there are 63 people on the train. How many people were on the train to begin with?
2. You’ll Never Forget Cheryl’s Birthday 📅
Country of origin: Singapore
Problems that test logical reasoning are common in Math(s) Olympiads. But this question from the 2015 Singapore and Asian Schools Math Olympiad contest for students 14 to 15 years old got the whole world stumped.
The Question:
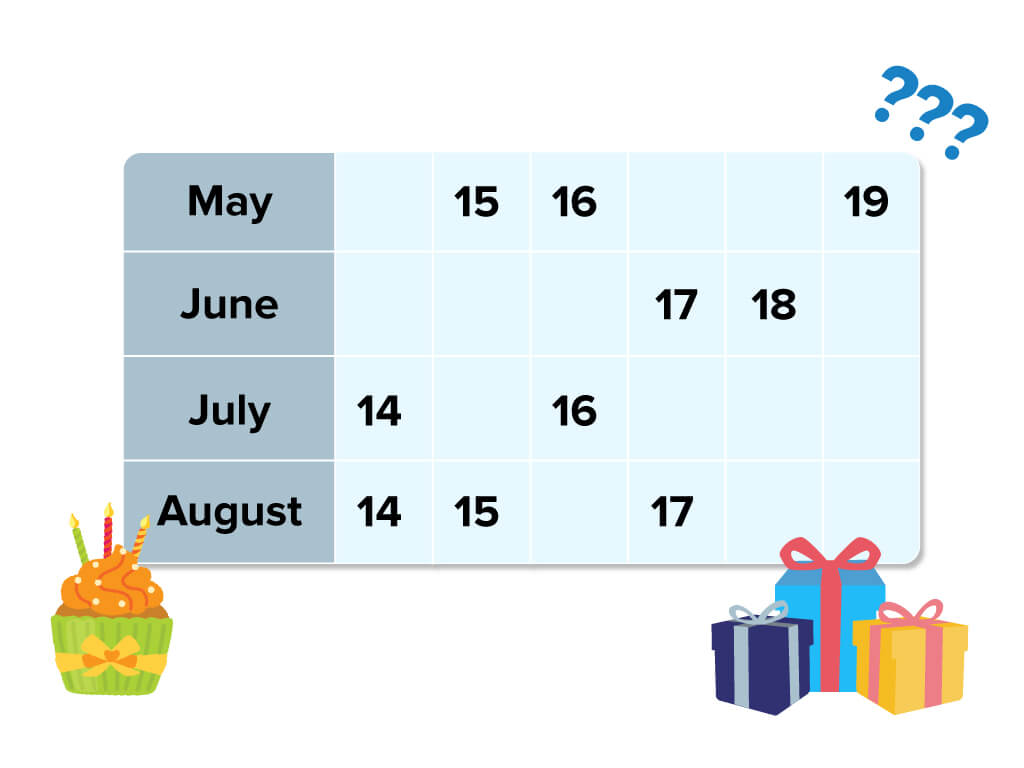
Albert and Bernard just became friends with Cheryl, and they want to know when her birthday is.
Cheryl gives them a list of 10 possible dates:
- May 15, May 16, May 19
- June 17, June 18
- July 14, July 16
- August 14, August 15, August 17
Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.
Albert: I don’t know when Cheryl’s birthday is, but I know that Bernard doesn’t know too.
Bernard: At first I don’t know when Cheryl’s birthday is, but I know now.
Albert: Then I also know when Cheryl’s birthday is.
So when is Cheryl’s birthday?
3. Taming the Snake 🐍
Country of origin: Vietnam
This question is not only tricky but might also take a while. According to VNEXPRESS, this puzzle is meant for third graders/year 3 students (8 year olds) in Vietnam!
The Puzzle:
Image source: VN Express
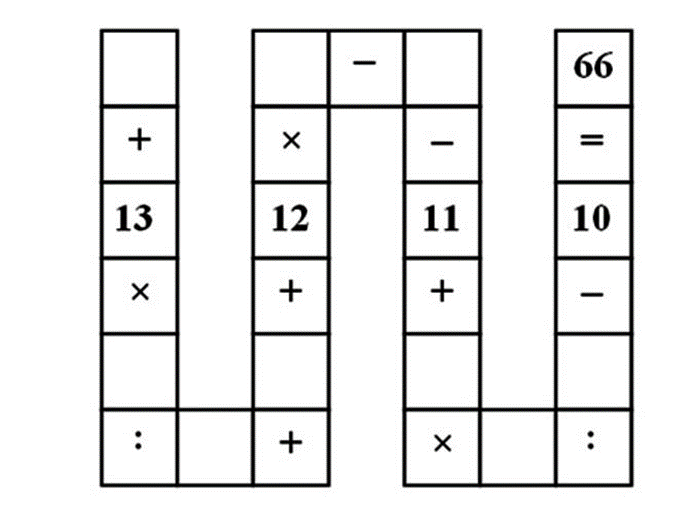
All you have to do is use the digit 1 to 9 once to fill in the boxes to make the entire equation equal to 66. The expression should be read from left to right.
Sounds easy? Not quite.
In case you’re wondering, the boxes containing colon represents division.
4. Remember Where You Parked Your Car 🚗
Country of origin: Hong Kong
This problem has been around for a while but resurfaced on an elementary/primary school entrance exam in Hong Kong.
Apparently, six-year-olds were expected to know the answer in 20 seconds or less.
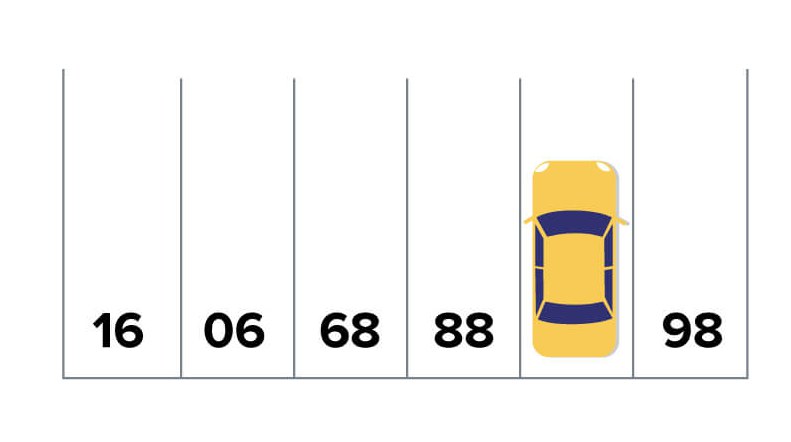
The Question:
What is the car’s parking spot number?
5. The Red Triangle 🔺
Country of origin: China
This question came from China and was used to identify gifted fifth grade/year 5 students (10 to 11 years old). It’s said that some of them were able to solve this question in less than one minute!
The Question:
ABCD is a parallelogram. In the diagram, the areas of yellow regions are 8, 10, 72 and 79.
Find the area of the red triangle. The diagram is not to scale.
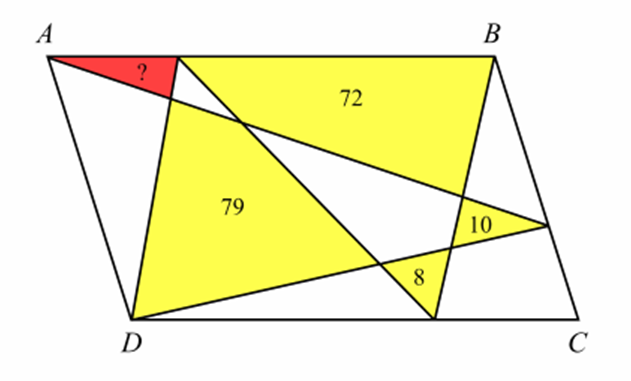
Image source: Mind Your Decisions
BONUS Tricky Math(s) Question
If you still have head space for one more, try this.
6. A Mass of Money: Helen and Ivan’s coins 💰

Country of origin: Singapore
In 2021, a Primary School Leaving Exam mathematics question left some 12-year-old students in tears. Supposedly, this question was meant to be solved in a matter of minutes, as it is only allocated 4 marks in total.
Note: This two-part question could have been recalled from memory and rewritten by an adult, which could explain the grammatical errors.
The Question:
Helen and Ivan had the same number of coins.
Helen had a number of 50-cent coins, and 64 20-cent coins. These coins had a mass of 1.134kg.
Ivan had a number of 50-cent coins and 104 20-cent coins.
(a) Who has more money in coins and by how much?
(b) given that each 50-cent coin is 2.7g heavier than a 20-cent coin, what is the mass of Ivan’s coins in kilograms?
Could You Solve These Tricky Mathematics Questions?
Or were you confused and stumped? Well, you’re not alone.
We had a really tough time understanding and solving them too.
If you’re a teacher and looking for problem and reasoning questions, consider a mathematics resource to sharpen your student’s logical thinking skills.
Now let’s get to the answers…
Question 1 Answer
19 people getting off the train can be represented by -19, and 17 people getting on the train as +17.
-19 + 17 = 2, meaning that there was a net loss of two people.
Originally, the train had 2 more people.
So if there are 63 people on the train now, that means there were 65 people to begin with.
Question 2 Answer
You can solve this by the process of elimination, based on what each person says.
Let’s go through the information line by line.
[Line 7] Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.
This is an important piece of information because it tells us that Albert knows the month, and Bernard knows the day.
So Albert knows it’s either May, June, July or August, and Bernard knows that it’s either 14, 15, 16, 17, 18 or 19.
[Line 8] Albert: I don’t know when Cheryl’s birthday is, but I know that Bernard doesn’t know too.
The second part is the clue. The fact that Albert claims that Bernard doesn’t know means it can’t be 18 or 19. Why?
If it were 19, then Bernard would know the exact birthday, as May is the only date with 19.
If Bernard was told the date was 18, he would also know that the birthday must be June 18, as that’s the only date with 18.
So you can rule out May 19 and June 18.
But how is Albert sure that Bernard didn’t hear 18 or 19?
It must be because Albert knows the birthday is not in May or June.
If Albert was told the month was May, he couldn’t be sure that Bernard wasn’t thinking of the number 19. Therefore, you can cross out May.
And if Albert was told the month of June, he couldn’t’ be sure if Bernard wasn’t thinking of the number 17. So June is also out.
In other words, Albert was told either July or August.
Based on the above information, you can eliminate these five dates – May 15, May 16, May 19, June 17 and June 18.
Dates left: July 14, July 16, August 14, August 15 and August 17.
[Line 9] Bernard: At first I don’t know when Cheryl’s birthday is, but now I know.
Upon hearing Albert’s statement, Bernard now figures this out.
If Bernard was told the date was 14, it would still be ambiguous whether the month was July or August. So you can rule out he was not told 14.
You are now left with three dates – July 16, August 15 and August 17.
[Line 10] Albert: Then I also know when Cheryl’s birthday is.
Albert couldn’t have been told it was August, as there are two dates in August. So you can deduce that he must have been told it’s July.
Therefore, the answer is July 16.
Question 3 Answer
Let’s start by breaking the puzzle into bite-size pieces, one step at a time.
First, write the expression in the normal way you usually write mathematical expressions. This makes it easier to put in the numbers.
__ + 13 × __ ÷ __ + __ + 12 × __ – __ – 11 + __ × __ ÷ __ – 10 = 66
Next, let’s look at how many ways are there to put the numbers 1 to 9 in these 9 different boxes.
You can put 9 different numbers in the first box.
So that’s 9 possibilities in the first box, 8 possibilities in the second box, followed by 7 boxes in the third box and so forth.
Applying this logic, you will have one less possibility for each box, until we get to the last box.
In total, there are 9 factorial (9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 9!) or 362,880 possibilities.
Now that’s a lot of possibilities to try and work by purely guessing and checking.
So let’s try working out the solution logically.
Step 1:
Remember the BEDMAS/BIDMAS/PEDMAS/PEMDAS rule you learnt in school?
To respect the order of operations, add parentheses or brackets to the equation. This means that multiplication or division comes before addition or subtraction.
__ + (13 × __ ÷ __) + __ + (12 × __) – __ – 11 + (__ × __ ÷ __) – 10 = 66
Step 2:
Now it’s time to fill in some numbers to guess and check our assumptions.
What if you first used the numbers 1 to 9, from left to right?
1 + (13 × 2 ÷ 3) + 4 + (12 × 5) – 6 – 11 + (7 × 8 ÷ 9) – 10 = 52.88…
Hey, that’s pretty close to 66!
What if you wrote the numbers in descending order, from 9 to 1?
9 + (13 × 8 ÷ 7) + 6 + (12 × 5) – 4 – 11 + (3 × 2 ÷ 1) – 10 = 70.85…
That also gets you pretty close to the answer.
So how can you modify this expression to get to 66? The key is to look at the numbers and their positions.
In the next few steps, we used trial and error – testing and moving the numbers around until we got to 66.
Here’s one solution we got:
9 + (13 × 4 ÷ 8) + 5 + (12 × 6) – 7 – 11 + (1 × 3 ÷ 2) – 10 = 66
Now for the keen observers out there, you’d notice that you can switch the numbers that are being added, to generate another solution.
For example:
9 + (13 × 4 ÷ 8) + 5 + (12 × 6) – 7 – 11 + (1 × 3 ÷ 2) – 10 = 66 OR (switch 5 and 9)
5 + (13 × 4 ÷ 8) + 9 + (12 × 6) – 7 – 11 + (1 × 3 ÷ 2) – 10 = 66
Similarly, you can switch the numbers that are multiplied, and it won’t affect the final answer.
9 + (13 × 4 ÷ 8) + 5 + (12 × 6) – 7 – 11 + (1 × 3 ÷ 2) – 10 = 66 OR (switch 1 and 3)
9 + (13 × 4 ÷ 8) + 5 + (12 × 6) – 7 – 11 + (3 × 1 ÷ 2) – 10 = 66
This means anytime you come up with one way to solve it, you can generate a total of four ways – because multipclation and addition are commutative (it doesn’t what the order of the numbers are, the answer is the same).
In fact, there are multiple answers to this puzzle. 136 to be exact. How do we know?
Now, that’s a problem to solve for another time. 😉
Question 4 Answer
The ‘trick’ to this question is that it requires no math(s) at all!
All you have to do is to look at it from a different perspective – literally.
Turn the question upside down, and you’ll see that it’s a simple number sequence, with the answer being 87.
Question 5 Answer
Even though it looks complicated, this question can actually be solved with a simple calculation:
79 + 10 – 72 – 8 = 9
Wait, what? But how?
To get there, you need to understand basic arithmetic and know that the area of a parallelogram and the area of a triangle are related.
The ‘secret’ is to identify triangles with areas that are half of the parallelogram.
The area of a triangle is (base × height) ÷ 2, and the area of a parallelogram is base × height.
A triangle whose base equals one side of the parallelogram, and whose height reaches the opposite side of the parallelogram, has exactly half the area of a parallelogram.
This is true for a pair of triangles as well – if the pair of triangles span one side and if their heights reach the opposite side.
To make solving this easier, you can start by labelling the unknown areas with letters a to f. And let the area of the red triangle be x.
Presh Talwalkar from Mind You Decisions, breaks down the solution in his video here.
Question 6 Answer (Part a)
The key is to remember that Helen and Ivan have the same number of coins.
Let’s look and compare the total number of coins for each type.
Ivan has 40 more 20-cent coins than Helen. For them to have the same number of coins, you have to ‘balance’ this out in terms of the 50-cent coins.
This means Helen must have 40 more of the 50-cent coins than Ivan.
Let’s now compare the amount of money of each coin type that Helen has, minus that of Ivan.
Since Helen has 40 fewer (104 – 64) of the 20-cent coins, so Helen will have:
– 40 × 0.2 = – 8
This means she has $8 less than Ivan (in 20-cent coins).
On the other hand, Helen has 40 more of the 50-cent coins than Ivan. So she will have:
+ 40 × 0.5 = 20
This means she has $20 more than Ivan (in 50-cent coins).
Now, you can add this together to find out how much more or less money Helen has.
– 8 + 20 = 12
Therefore, Helen has $12 more than Ivan.
Question 6 Answer (Part b):
The total mass of Helen’s coin is 1.134kg. And you know that a 50-cent coin is 2.7g heavier than a 20-cent coin.
From the first part of the question, you can see that if you had Helen’s coins, you can ‘exchange’ 40 of the 50-cent coins for 40 of the 20-cent coins, that will be the total coins Ivan has. And you can get the weight difference from that.
Let’s compare the weight of Helen’s coins to Ivan’s coins.
In terms of the 20-cent coins, subtract 40 of the 20-cent coins, multiplied by the weight of the coins.
– 40 × 0.2 weight
In terms of the 50-cent coins, add 40 of the 50-cent coins, multiplied by the weight.
+40 × 0.5 weight
So the net impact of this, Helen compared to Ivan, has 40 more of the heavier coins – 40 more of the 50-cent coins, compared to the 20-cent coins than Ivan.
+ 40 × 0.5 weight / 40 × (0.5 – 0.2 weight)
You know the difference in weight between 50-cent and 20-cent coins is 2.7 grams. Therefore, you can substitute that in the equation.
+ 40 × 0.5 weight / 40 × (2.7 g) –> 40 × (2.7 g) = 108g
So Helen’s weight of coins is 108 g more than Ivan.
To get Ivan’s weight, we take Helen’s coins and subtract by 108g.
1134g – 108g = 1026g
Convert that to kilograms to get the answer, 1.026 kg.
How did you fare? Share this with your students or friends who love a great math(s) challenge!
If you’re looking to challenge your students’ mathematical fluency, why not take part if World Maths Day – the world’s largest online competition?