Finding Soft Skills in Mathematics Isn’t As Hard As You Might Think

With its focus on problem-solving, reasoning, and complex communication, maths brings out many of the soft skills that will set our students up for a fast-changing future.

But for teachers who deal in hard skills – facts, formulas, and procedures – actually developing students’ grasp of these soft skills can seem impossibly ambiguous.

Teaching fractions is one thing, but how do you ‘teach’ students to become better communicators? Or more reflective thinkers?

That’s the question we’ll answer below, but before we do, a recap:

Soft skills are general competencies that aren’t specific to any particular subject. For example:

• communication
• resilience
• collaboration
• reasoning
• problem-solving.

All of these skills are transferable across different disciplines and scenarios. That’s why they’re the best investment for students heading into a world where new careers are being created every day.

But the best part?

Maths exercises almost all of them. And by actively developing these soft skills, you’ll future-proof your students’ professional and personal journeys.

Here are 5 strategies for doing just that.

If you explicitly discuss skills like ‘problem-solving’, ‘reasoning’, and ‘reflecting’, they’ll start to become an ingrained part of your students’ thinking.

Call them by name, teach their meanings, and provide examples of where these skills might be used in and out of the classroom.

An effective way to introduce this language is to…

Next time you’re demonstrating your approach to a problem on the board, talk your students through the thinking process as well as the procedures being used. Break it down into specifics like:

“I’m thinking I’ll try this particular problem-solving strategy because…”

“That didn’t work, so instead I’m going to try…”

“I can tell that this is asking me to… because“

This allows you to give a live demonstration of soft skills in action, such as:

• communicating thinking
• problem-solving
• reasoning
• monitoring and checking for accuracy.

Group work is your best opportunity to develop students’ collaborative skills. Get the most out of it by:

Using the puzzle piece approach

In the puzzle piece approach, the group has a shared problem-solving activity, and each student is given a unique clue to contribute.

For example, let’s assume students have to find a mystery number where the answer is 18. Each group member receives one of the following clues:

• The number is a multiple of 6.
• The number is even.
• The number is less than 20.
• When you add the digits together you get a multiple of 3.

Because every group member has something to contribute, shy students get the chance to speak up, and big talkers are encouraged to listen.

Using group norms during collaborative tasks

Most students struggle with collaboration because they don’t understand it.

That’s why group norms, which explicitly spell out the ‘rules’ of collaboration, are so effective.

Here’s an example set you can apply to any collaborative activity:

• One person speaks at any given time.
• After someone speaks, take 5 seconds to silently process what they’ve said.
• When disagreeing with someone else, begin with ‘I hear what you’re saying’.
• If you wish to speak, put your hand up and wait for the facilitator to call on you.
• Treat others with courtesy and respect.

A number talk is a verbal explanation of how a mathematical problem can be solved. It develops students’ ability to:

• communicate complex concepts
• reflect on their own thinking
• select and articulate problem-solving strategies.

So next time a student fires off a correct answer, get them talking about how they reached it. Use open-ended questions such as:

• How many ways could you attempt to solve the problem?
• Why did you choose to approach it in that way?
• Which parts gave you a clue that this was a [division] problem?
• Why does that work?
• What happens if you try a different method?

Once you get students talking about maths – as opposed to just doing it – the soft skills behind their mathematical activity will gradually become more visible.

In the world outside the classroom, problems rarely have a single answer. Nor are they written down with symbols that tell students exactly what procedures are required.

Instead, they require students to:

• think creatively
• trial different problem-solving strategies
• find patterns and connections
• self-monitor and check their thinking.

Use challenging open-ended problems to develop these soft skills. These could be visual, word-based, or interactive. Take the following example for spatial reasoning:

Mr Stearns has a rose garden with 3 different types of roses. Each rose is in its own square of wooden planks, so it looks like this:

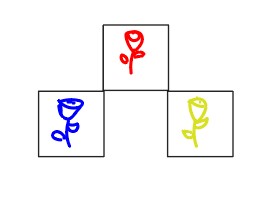
Mr Stearns has just bought another type of rose, and it needs its own square. How can he make 4 squares by moving 3 planks?

Students have to trial different strategies in order to find one that works. For example, they might begin by moving three conjoined planks as a single unit, but then discover that it’s easier solved if they split planks and move them to different places.

They’ll also experiment with broader problem-solving strategies – perhaps beginning by imagining the spatial transformation, and then diagramming it on a piece of paper.

Creating problems to develop soft skills

If you’re going to create your own problem-solving activities to develop student soft skills, make sure they have the following characteristics:

1. more than one possible answer
2. more than one strategy for reaching an answer
3. no symbols or words that tell students which procedure to use.

But if writing original, challenging problems takes time you don’t have, consider sourcing them from a digital program. For example, our secondary maths program, Mathletics, contains over 700 problem-solving activities to suit students up to Year 10. Get access to them all for free via the link below.